Diesel Cycle Example¶
Imports¶
[1]:
from thermostate import State, Q_, units
from thermostate.plotting import IdealGas
%matplotlib inline
import matplotlib.pyplot as plt
from numpy import arange
Definitions¶
[2]:
substance = "air"
T_1 = Q_(25.0, "degC")
p_1 = Q_(95.0, "kPa")
V_1 = Q_(3.0, "L")
r = Q_(18.0, "dimensionless")
r_c = Q_(3.0, "dimensionless")
rpm = Q_(1700.0, "rpm")
n_C = Q_(4, "dimensionless")
units.define("cycle = 2*revolution") # Define a four-stroke cycle
r_c_low = Q_(1.1, "dimensionless")
r_c_high = Q_(4.5, "dimensionless")
Problem Statement¶
A four-cylinder Diesel engine has a BDC volume of 3.0 L per cylinder. The engine operates on the air-standard Diesel cycle with a compression ratio of 18.0 and a cutoff ratio of 3.0 . Air is at 25.0 celsius and 95.0 kPa at the beginning of the compression process. Determine
the amount of power delivered by the engine, in kW, at 1700.0 rpm
the thermal efficiency
plot the power output as a function of the cutoff ratio, with values for \(r_c\) from 1.1 to 4.5 , holding all other given values constant
plot the thermal efficiency as a function of the cutoff ratio, with values for \(r_c\) from 1.1 to 4.5 , holding all other given values constant
Solution¶
1. the power delivered¶
The power output can be found by taking the product of the net work per cylinder, the number of cylinders, and the net work per revolution
\[\dot{W}_{net} = n_C \frac{N}{2} W_{net}\]
First, we need to fix the four states. State 1 uses \(p\) and \(T\), state 2 uses \(s\) and \(v\), state 3 uses \(p\) and \(v\), and state 4 uses \(v\) and \(s\). We need to calculate the mass of air in one cylinder using the ideal gas law
\[m = \frac{pV}{RT}\]
where \(R=\overline{R}/MW\) is the gas-specific constant.
The Diesel cycle is made of 4 processes:
1. Isentropic compression
2. Isobaric heat input
3. Isentropic expansion
4. Isochoric heat rejection
The following properties are used to fix the four states:
State |
Property 1 |
Property 2 |
|---|---|---|
1 |
\[p_1\]
|
\[T_1\]
|
2 |
\[v_2 = v_1/r\]
|
\[s_2=s_1\]
|
3 |
\[p_3=p_2\]
|
\[v_3=r_c*v_2\]
|
4 |
\[v_4=v_1\]
|
\[s_4=s_3\]
|
[3]:
MW_air = Q_(28.97, "kg/kmol")
R = units.molar_gas_constant / MW_air
m = (p_1 * V_1 / (R * T_1)).to("mg")
v_1 = (V_1 / m).to("m**3/kg")
st_1 = State(substance, p=p_1, T=T_1)
s_1 = st_1.s.to("kJ/(kg*K)")
u_1 = st_1.u.to("kJ/kg")
v_2 = v_1 / r
s_2 = s_1
st_2 = State(substance, v=v_2, s=s_2)
T_2 = st_2.T
p_2 = st_2.p.to("kPa")
u_2 = st_2.u.to("kJ/kg")
v_3 = r_c * v_2
p_3 = p_2
st_3 = State(substance, p=p_3, v=v_3)
T_3 = st_3.T
s_3 = st_3.s.to("kJ/(kg*K)")
u_3 = st_3.u.to("kJ/kg")
s_4 = s_3
v_4 = st_1.v
st_4 = State(substance, v=v_4, s=s_4)
T_4 = st_4.T
p_4 = st_4.p.to("kPa")
u_4 = st_4.u.to("kJ/kg")
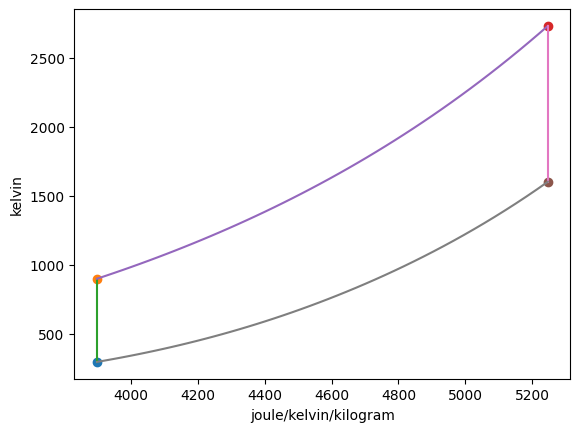
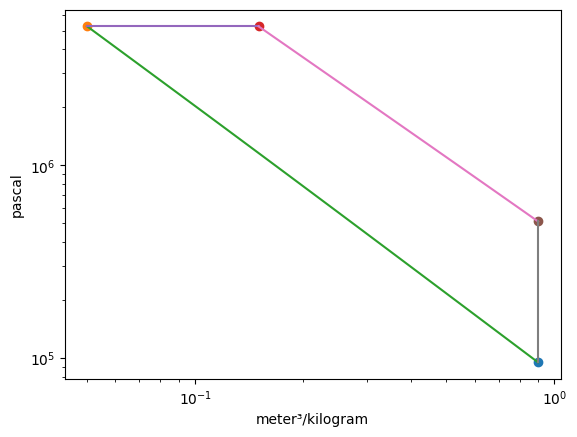
Plotting the p-v and T-s diagrams of the cycle,
[4]:
Diesel = IdealGas(substance, ("s", "T"), ("v", "p"))
Diesel.add_process(st_1, st_2, "isentropic")
Diesel.add_process(st_2, st_3, "isobaric")
Diesel.add_process(st_3, st_4, "isentropic")
Diesel.add_process(st_4, st_1, "isochoric")
The mass of air in one cylinder is \(m =\) 3330.61 mg. Summarizing the states:
State |
T |
p |
u |
v |
s |
|---|---|---|---|---|---|
1 |
298.15 K |
95.00 kPa |
338.89 kJ/kg |
0.90 m3/kg |
3.90 kJ/(K kg) |
2 |
900.45 K |
5256.76 kPa |
799.36 kJ/kg |
0.05 m3/kg |
3.90 kJ/(K kg) |
3 |
2730.75 K |
5256.76 kPa |
2522.03 kJ/kg |
0.15 m3/kg |
5.25 kJ/(K kg) |
4 |
1602.36 K |
511.21 kPa |
1426.75 kJ/kg |
0.90 m3/kg |
5.25 kJ/(K kg) |
[5]:
W_12 = (m * (u_1 - u_2)).to("kJ")
W_23 = (m * p_2 * (v_3 - v_2)).to("kJ")
W_34 = (m * (u_3 - u_4)).to("kJ")
W_net = W_12 + W_23 + W_34
Q_23 = (m * (u_3 - u_2) + W_23).to("kJ")
Q_41 = (m * (u_1 - u_4)).to("kJ")
Summarizing the energy transfers,
Process |
Work |
Heat Transfer |
|---|---|---|
1 \(\rightarrow\) 2 |
-1.53 kJ |
0.0 kJ |
2 \(\rightarrow\) 3 |
1.75 kJ |
7.49 kJ |
3 \(\rightarrow\) 4 |
3.65 kJ |
0.0 kJ |
4 \(\rightarrow\) 1 |
0.0 kJ |
-3.62 kJ |
and the net work output per cylinder per cycle is \(W_{net} =\) 3.87 kJ. Then, calculating the power output
[6]:
Wdot_net = (n_C * rpm * W_net / units.cycle).to("kW")
Answer: The net power output is \(\dot{W}_{net} =\) 219.10 kW
2. the thermal efficiency¶
[7]:
eta = W_net / Q_23
Answer: The thermal efficiency is \(\eta =\) 0.52 = 51.62%
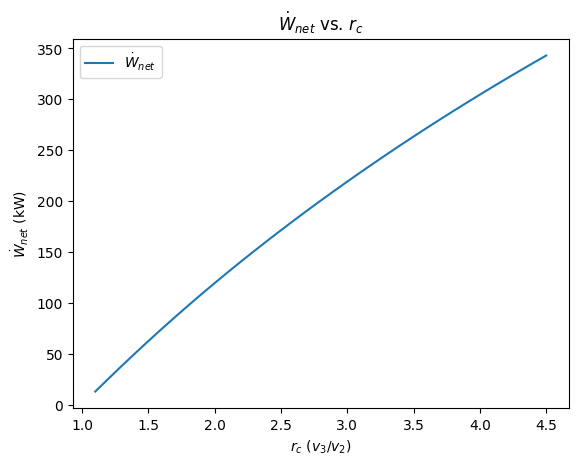
3. plot the net power output as a function of \(r_c\)¶
For this part (and the next one), only states 3 and 4 are changed by changing the cutoff ratio. Therefore, we only re-compute those states, and the associated work and heat transfer values, in the following loop.
[8]:
eta_l = []
Wdot_net_l = []
r_c_l = arange(r_c_low.magnitude, r_c_high.magnitude + 0.1, 0.1)
for r_c in r_c_l:
v_3 = r_c * v_2
p_3 = p_2
st_3 = State(substance, p=p_3, v=v_3)
s_3 = st_3.s.to("kJ/(kg*K)")
u_3 = st_3.u.to("kJ/kg")
s_4 = s_3
v_4 = v_1
st_4 = State(substance, v=v_4, s=s_4)
u_4 = st_4.u.to("kJ/kg")
W_23 = (m * p_2 * (v_3 - v_2)).to("kJ")
W_34 = (m * (u_3 - u_4)).to("kJ")
W_net = W_12 + W_23 + W_34
Wdot_net = (n_C * rpm * W_net / units.cycle).to("kW")
Wdot_net_l.append(Wdot_net.magnitude)
Q_23 = (m * (u_3 - u_2) + W_23).to("kJ")
eta = W_net / Q_23
eta_l.append(eta.magnitude)
---------------------------------------------------------------------------
ValueError Traceback (most recent call last)
Cell In[8], line 7
5 v_3 = r_c * v_2
6 p_3 = p_2
----> 7 st_3 = State(substance, p=p_3, v=v_3)
8 s_3 = st_3.s.to("kJ/(kg*K)")
9 u_3 = st_3.u.to("kJ/kg")
File ~/checkouts/readthedocs.org/user_builds/thermostate/envs/stable/lib/python3.10/site-packages/thermostate/thermostate.py:319, in State.__init__(self, substance, label, units, **kwargs)
313 raise StateError(
314 f"The pair of input properties entered ({input_props}) isn't supported "
315 "yet. Sorry!"
316 )
318 if len(input_props) > 0:
--> 319 setattr(self, input_props, (kwargs[input_props[0]], kwargs[input_props[1]]))
File ~/checkouts/readthedocs.org/user_builds/thermostate/envs/stable/lib/python3.10/site-packages/thermostate/thermostate.py:226, in State.__setattr__(self, key, value)
224 self._check_dimensions(key, value)
225 self._check_values(key, value)
--> 226 self._set_properties(key, value)
227 elif key in self._unsupported_pairs:
228 raise StateError(
229 f"The pair of input properties entered ({key}) isn't supported yet. "
230 "Sorry!"
231 )
File ~/checkouts/readthedocs.org/user_builds/thermostate/envs/stable/lib/python3.10/site-packages/thermostate/thermostate.py:411, in State._set_properties(self, known_props, known_values)
409 inputs = getattr(CoolProp, "".join(known_state.keys()) + "_INPUTS")
410 try:
--> 411 self._abstract_state.update(inputs, *known_state.values())
412 except ValueError as e:
413 if "Saturation pressure" in str(e):
File CoolProp/AbstractState.pyx:106, in CoolProp.CoolProp.AbstractState.update()
File CoolProp/AbstractState.pyx:108, in CoolProp.CoolProp.AbstractState.update()
ValueError: argument not found
[9]:
plt.figure()
plt.plot(r_c_l, Wdot_net_l, label="$\dot{W}_{net}$")
plt.legend(loc="best")
plt.title("$\dot{W}_{net}$ vs. $r_c$")
plt.xlabel("$r_c$ ($v_3/v_2$)")
plt.ylabel("$\dot{W}_{net}$ (kW)");
---------------------------------------------------------------------------
ValueError Traceback (most recent call last)
Cell In[9], line 2
1 plt.figure()
----> 2 plt.plot(r_c_l, Wdot_net_l, label="$\dot{W}_{net}$")
3 plt.legend(loc="best")
4 plt.title("$\dot{W}_{net}$ vs. $r_c$")
File ~/checkouts/readthedocs.org/user_builds/thermostate/envs/stable/lib/python3.10/site-packages/matplotlib/pyplot.py:3838, in plot(scalex, scaley, data, *args, **kwargs)
3830 @_copy_docstring_and_deprecators(Axes.plot)
3831 def plot(
3832 *args: float | ArrayLike | str,
(...)
3836 **kwargs,
3837 ) -> list[Line2D]:
-> 3838 return gca().plot(
3839 *args,
3840 scalex=scalex,
3841 scaley=scaley,
3842 **({"data": data} if data is not None else {}),
3843 **kwargs,
3844 )
File ~/checkouts/readthedocs.org/user_builds/thermostate/envs/stable/lib/python3.10/site-packages/matplotlib/axes/_axes.py:1777, in Axes.plot(self, scalex, scaley, data, *args, **kwargs)
1534 """
1535 Plot y versus x as lines and/or markers.
1536
(...)
1774 (``'green'``) or hex strings (``'#008000'``).
1775 """
1776 kwargs = cbook.normalize_kwargs(kwargs, mlines.Line2D)
-> 1777 lines = [*self._get_lines(self, *args, data=data, **kwargs)]
1778 for line in lines:
1779 self.add_line(line)
File ~/checkouts/readthedocs.org/user_builds/thermostate/envs/stable/lib/python3.10/site-packages/matplotlib/axes/_base.py:297, in _process_plot_var_args.__call__(self, axes, data, return_kwargs, *args, **kwargs)
295 this += args[0],
296 args = args[1:]
--> 297 yield from self._plot_args(
298 axes, this, kwargs, ambiguous_fmt_datakey=ambiguous_fmt_datakey,
299 return_kwargs=return_kwargs
300 )
File ~/checkouts/readthedocs.org/user_builds/thermostate/envs/stable/lib/python3.10/site-packages/matplotlib/axes/_base.py:494, in _process_plot_var_args._plot_args(self, axes, tup, kwargs, return_kwargs, ambiguous_fmt_datakey)
491 axes.yaxis.update_units(y)
493 if x.shape[0] != y.shape[0]:
--> 494 raise ValueError(f"x and y must have same first dimension, but "
495 f"have shapes {x.shape} and {y.shape}")
496 if x.ndim > 2 or y.ndim > 2:
497 raise ValueError(f"x and y can be no greater than 2D, but have "
498 f"shapes {x.shape} and {y.shape}")
ValueError: x and y must have same first dimension, but have shapes (35,) and (22,)
4. plot \(\eta\) vs. \(r_c\)¶
[10]:
plt.figure()
plt.plot(r_c_l, eta_l, label="$\eta$")
plt.legend(loc="best")
plt.title("$\eta$ vs. $r_c$")
plt.xlabel("$r_c$ ($v_3/v_2$)")
plt.ylabel("$\eta$");
---------------------------------------------------------------------------
ValueError Traceback (most recent call last)
Cell In[10], line 2
1 plt.figure()
----> 2 plt.plot(r_c_l, eta_l, label="$\eta$")
3 plt.legend(loc="best")
4 plt.title("$\eta$ vs. $r_c$")
File ~/checkouts/readthedocs.org/user_builds/thermostate/envs/stable/lib/python3.10/site-packages/matplotlib/pyplot.py:3838, in plot(scalex, scaley, data, *args, **kwargs)
3830 @_copy_docstring_and_deprecators(Axes.plot)
3831 def plot(
3832 *args: float | ArrayLike | str,
(...)
3836 **kwargs,
3837 ) -> list[Line2D]:
-> 3838 return gca().plot(
3839 *args,
3840 scalex=scalex,
3841 scaley=scaley,
3842 **({"data": data} if data is not None else {}),
3843 **kwargs,
3844 )
File ~/checkouts/readthedocs.org/user_builds/thermostate/envs/stable/lib/python3.10/site-packages/matplotlib/axes/_axes.py:1777, in Axes.plot(self, scalex, scaley, data, *args, **kwargs)
1534 """
1535 Plot y versus x as lines and/or markers.
1536
(...)
1774 (``'green'``) or hex strings (``'#008000'``).
1775 """
1776 kwargs = cbook.normalize_kwargs(kwargs, mlines.Line2D)
-> 1777 lines = [*self._get_lines(self, *args, data=data, **kwargs)]
1778 for line in lines:
1779 self.add_line(line)
File ~/checkouts/readthedocs.org/user_builds/thermostate/envs/stable/lib/python3.10/site-packages/matplotlib/axes/_base.py:297, in _process_plot_var_args.__call__(self, axes, data, return_kwargs, *args, **kwargs)
295 this += args[0],
296 args = args[1:]
--> 297 yield from self._plot_args(
298 axes, this, kwargs, ambiguous_fmt_datakey=ambiguous_fmt_datakey,
299 return_kwargs=return_kwargs
300 )
File ~/checkouts/readthedocs.org/user_builds/thermostate/envs/stable/lib/python3.10/site-packages/matplotlib/axes/_base.py:494, in _process_plot_var_args._plot_args(self, axes, tup, kwargs, return_kwargs, ambiguous_fmt_datakey)
491 axes.yaxis.update_units(y)
493 if x.shape[0] != y.shape[0]:
--> 494 raise ValueError(f"x and y must have same first dimension, but "
495 f"have shapes {x.shape} and {y.shape}")
496 if x.ndim > 2 or y.ndim > 2:
497 raise ValueError(f"x and y can be no greater than 2D, but have "
498 f"shapes {x.shape} and {y.shape}")
ValueError: x and y must have same first dimension, but have shapes (35,) and (22,)
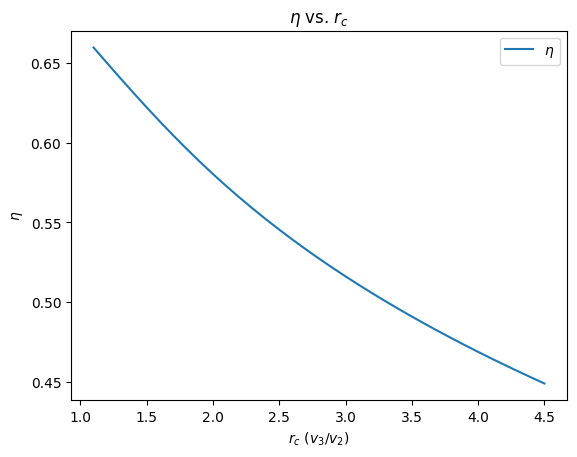
From these graphs, we note that as the cutoff ratio increases, the power delivered increases but the thermal efficiency decreases.
